Data Structure: Graph
Graph란
Graph는 현실 세계에 존재하는 사물, 현상 등(객체)간의 관계를 표현하는 자료구조이며, 노드(Node)와 엣지(Edge)로 구성되어 있습니다.
ex) 지하철 노선도, 지도, 쾨니히스베르그의 다리 등
노드(Node)는 객체로 정점, 꼭짓점(vertex) 등으로 표현하며, 간선(Edge)은 객체간의 관계로 원들을 잇는 선(line)으로 표현합니다.

Graph의 종류
Graph의 종류를 다음과 같이 간단하게 알아보겠습니다.
더 많은 종류는 다음 링크를 참조하시면 좋을 것 같습니다.
https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html
- 무방향 그래프(Undirected Graph)
- 무방향 그래프는 간선(Edge)을 통해 어느 방향이든 이동이 가능합니다.
- 예를 들어 정점(vertex) A와 B를 연결하는 간선은 (A, B) 또는 (B, A)와 같이 정점의 쌍으로 표현합니다.
- 방향 그래프(Directed Graph)
- 방향 그래프는 간선에 방향성이 존재합니다.
- A에서 B로만 갈 수 있는 간선(A->B)은 <A, B>로 표시합니다.

Graph의 표현
- 인접 리스트(Adjacency List)
- 모든 정점(node)를 인접 리스트에 저장 즉, 각각의 정점에 인접한 정점들을 리스트로 표시한 것입니다.
- 인접 행렬(Adjacency Matrix)
- 인접 행렬은 N*N 크기의 Boolean Matrix로써 matrix[i][j]가 true라면 i -> j로의 간선이 있다는 뜻입니다.
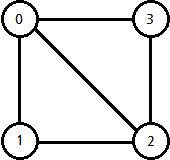
- 인접 행렬은 N*N 크기의 Boolean Matrix로써 matrix[i][j]가 true라면 i -> j로의 간선이 있다는 뜻입니다.
인접 행렬 vs 인접 리스트
| 인접 행렬 | 인접 리스트 | |
|---|---|---|
| 접근성 | 빠름 | 느림 |
| 메모리 | 많이소모 | 적게소모 |
Graph 탐색
1) 깊이 우선 탐색(DFS, Depth-First Search)
- 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 완벽하게 탐색하는 방법
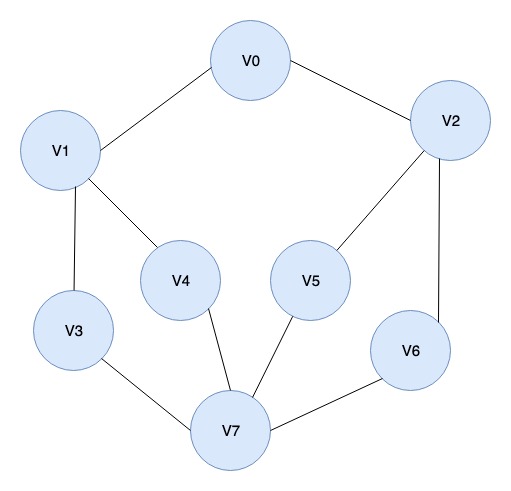
- 1.그래프의 시작 지점(V0)에서 출발하여 먼저 시작 지점 노드를 방문하였다고 표시합니다.
- 2.그리고 V0에 인접한 노드들을 차례로 방문합니다. 만약 방문할 노드가 없다면 탐색을 종료합니다.
- 3.만약 V0에 인접한 V1을 방문하였다면, V0에 인접한 다른 노드들을 방문하기 전에 V1에 인접한 노드들을 먼저 차례로 방문해야 합니다.
- 4.위 3번과 같이 다음 방문 노드에서 인접한 노드들을 먼저 차례로 방문한 후 방문할 노드가 없다면 backtracking하여 탐색하지 않은 노드가 있는지 확인합니다.
2) 너비 우선 탐색(BFS, Breadth-First Search)
- 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법

- 1.그래프의 시작 지점(V0)에서 출발하여 먼저 시작 지점 노드를 방문하였다고 표시합니다.
- 2.그리고 V0에 인접한 노드들을 먼저 차례로 방문합니다. 만약 방문할 노드가 없다면 탐색을 종료합니다.
- 3.V0가 인접한 노드를 모두 방문한 후, 인접한 V1, V2, V3 노드 중 하나를 선택하여 해당 노드를 출발점으로 다시 1,2번을 반복합니다.

